A group of researchers using the Suprime-Cam instrument on the Subaru Telescope has discovered about 80 young galaxies that existed in the early universe about 1.2 billion years after the Big Bang. The team, with members from Ehime University, Nagoya University, Tohoku University, Space Telescope Science Institute (STScI) in the U.S., and California Institute of Technology, then made detailed analyses of imaging data of these galaxies taken by the Advanced Camera for Surveys (ACS) on the Hubble Space Telescope. At least 54 of the galaxies are spatially resolved in the ACS images. Among them, 8 galaxies show double-component structures (Figure 1) and the remaining 46 seem to have elongated structures (Figure 2). Through a further investigations using a computer simulation, the group found that the observed elongated structures can be reproduced if two or more galaxies reside in close proximity to each other.
These results strongly suggest that 1.2 billion years after the Big Bang, galactic clumps in the young universe grow to become large galaxies through mergers, which then causes active star formation to take place. This research was conducted as part of the treasury program of Hubble Space Telescope (HST), "Cosmic Evolution Survey (COSMOS)". The powerful survey capability of the Subaru Telescope provided the essential database of the candidate objects in the early universe for this research project.

Figure 1: An example of galaxy that shows a double-component structure in the HST/ACS image. North is up and east is left. Each panel has a size of 4" x 4", which corresponds to 85 kly x 85 kly at the distance of 12.6 billion light-years. The thumbnails of the HST/ACS I band (effective wavelength = 814 nm), the Subaru Telescope/Suprime-Cam NB711 and i'- and z'-bands are shown from left to right. Note that the NB711 image, which captures the Lyman-alpha line emitted by neutral hydrogen, shows spatially extended gas which is ionized by ultraviolet (UV) radiation from many massive stars. On the other hand, other band images prove the UV radiation from massive stars themselves. (Credit: Ehime University)
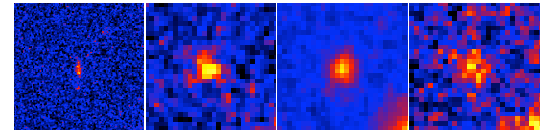
Figure 2: Same as Figure 1 but for an example of galaxy that shows a single-component structure in the HST/ACS image. (Credit: Ehime University)
The Importance of Studying Early Galaxies
In the present universe, at a point 13.8 billion years after the Big Bang, there are many giant galaxies like our Milky Way, which contains about 200 billion stars in a disk a hundred thousand light years across. However, there were definitely no galaxies like it in the epoch just after the Big Bang.
Pre-galactic clumps appear to have formed in the universe about 200 million years after the Big Bang. These were cold gas clouds much smaller than the present giant galaxies by a factor of 100, with masses smaller by a factor of a million. The first galaxies were formed when the first stars were born in these gas clumps. These small galactic clumps then experienced continuous mergers with surrounding clumps and eventually grew into large galaxies.
Much effort has been made through deep surveys to detect actively star-forming galaxies in the young universe. As a result, the distances of the earliest galaxies are now known to be at more than 13 billion light-years. We see them at a time when the age of the universe was only 800 million years (or about 6% of the present age). However, since most of the galaxies in the young universe were quite small, their detailed structures have not yet been observed.
Exploring the Young Universe Using Subaru Telescope and Hubble Space Telescope
While the wide field of view of the Subaru Telescope has played an important role in finding such young galaxies, the high spatial resolution of the Hubble Space Telescope (HST) is required to investigate the details of their shapes and internal structures. The research team looked back to a point 12.6 billion years ago using a two-pronged approach. The first step was to use the Subaru Telescope in a deep survey to search out the early galaxies, and then follow that up to investigate their shapes using the Advanced Camera for Surveys (ACS) on board the HST. The ACS revealed 8 out of 54 galaxies to have double-component structures, where two galaxies seem to be merging with each other (Note 1), as shown in Figure 1.Then, a question arose as to whether the remaining 46 galaxies are really single galaxies. Here, the research team questioned why many of these galaxies show elongated shapes in the HST/ACS images (Figure 2). This is because such elongated shapes, together with the positive correlation between ellipticity (Note 2) and size (Figure 3), strongly suggest a possibility that two small galaxies reside so close to each other that they cannot be resolved into two distinct galaxies, even using ACS.
To examine whether the idea of closely crowded galaxies is viable, the researchers conducted so-called Monte Carlo computer simulations. First, the group put two identical artificial sources at random locations with various angular separations onto the real observed ACS image. Then, the group tried to extract the images with the same method used for the actual observed ACS image and measured their ellipticities and sizes. The results are shown in Figure 3.

Figure 3: The relation between ellipticity and size. Red data points are the observed data; most of them have elongated shapes and larger galaxies tend to have larger ellipticities. Gray-colored regions represent the probability distributions calculated with the computer simulations, in which two galaxies are located at so close distance that they are blended as an elongated galaxy, as shown in the right pictures schematically. (Credit: Ehime University)
As shown in Figure 3, the simulated distribution reproduces the observed results very well. That is, most of the galaxies that were observed as single sources in the HST/ACS images are actually two merging galaxies. However, the distances between two merging galaxies are so small they cannot be spatially resolved, even by HST's high resolution!
If this idea is valid for the galaxies that appear to be single, then it's possible to assume that the galaxies with the highest rate of activities have the smallest sizes. This is expected because the smallest sizes imply the smallest separation between two merging galaxies. If this is the case, such galaxies would experience intense star formation activity triggered by their mergers.
On the other hand, some galaxies with the smallest sizes are moderately separated pairs, but are observed along the line of sight, or are just single, isolated star-forming galaxies. These are basically the same as large-size galaxies.
The research team has confirmed that the observed relation between star formation activity and size is consistently explained by the team's idea (Figure 4).
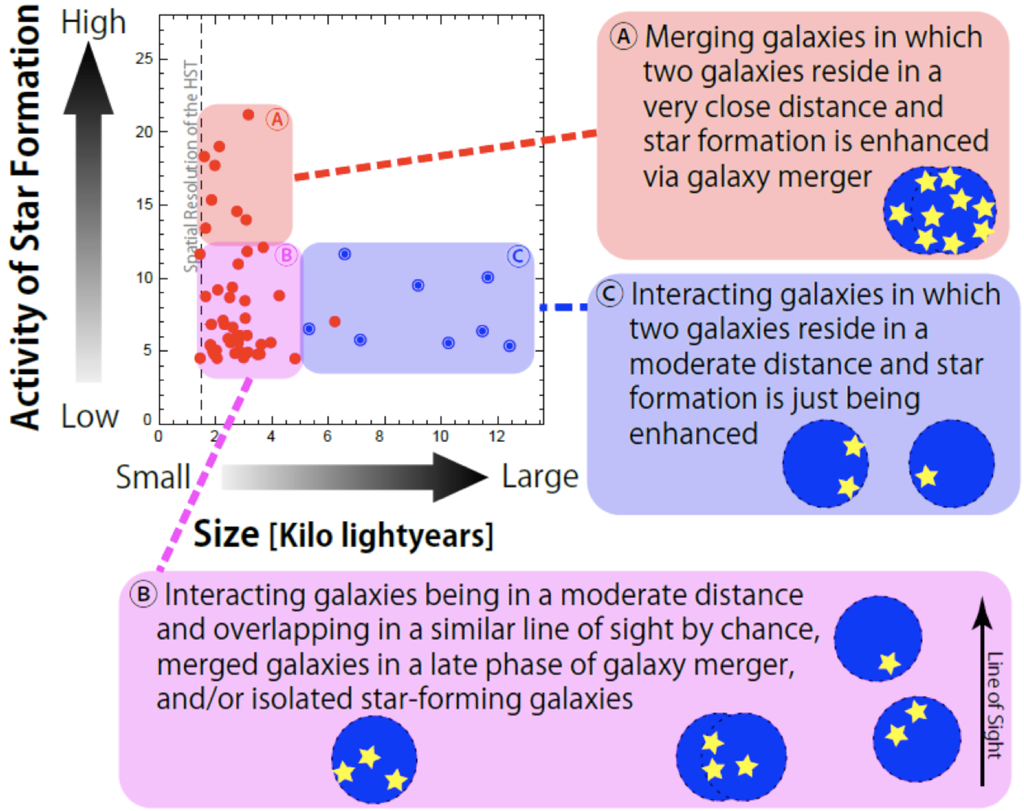
Figure 4: The relation between star formation activity and size. Red circles and blue double-circles represent the galaxies with single- and double-component ACS sources, respectively. The research team's idea that most of the galaxies consist of two (or more) interacting small galaxies with small angular separation is also illustrated, which explains the observed trend very well. (Credit: Ehime University)
To date, the shapes and structures of small young galaxies have been investigated by using ACS on HST. If a source was detected as a single ACS source, it was treated as a single galaxy and its morphological parameters were evaluated. This research suggests that such a small galaxy can consist of two (or perhaps, more) interacting/merging galaxies located so close together that they cannot be resolved by even the high angular resolution of the ACS.
Looking into the Future of Studying the Past
Current galaxy formation theories predict that small galaxies in the young universe evolve into large galaxies via successive mergers. The question remains: what is the next step in observational studies for galaxy formation in the young universe? This is one of the frontier fields that requires future "super telescopes," e.g. Thirty Meter Telescope (TMT) and the James Webb Space Telescope (JWST). They will enable the next breakthroughs in the study of early galaxy formation and evolution.This research will be published in the Astrophysical Journal titled "Morphological Properties of Lyman Alpha Emitters at Redshift 4.86 in the COSMOS Field: Clumpy Star Formation or Merger?" by Masakazu A. R. Kobayashi, Katsuhiro L. Murata, Anton M. Koekemoer, Takashi Murayama, Yoshiaki Taniguchi, Masaru Kajisawa, Yasuhiro Shioya, Nick Z. Scoville, Tohru Nagao, and Peter L. Capak. Online version was posted February 24, 2016 and print version was on March 1, 2016 (Volume 819, article id. 25).
Note:
1.A mean size (that is, a mean diameter of the circle which encloses half of the total light of galaxy) of individual small galaxies is about 5.5 thousand light-years (kly). A mean distance between the two small galaxies, which is projected distance on the sky, is 13 kly (13,000 light-years).2.Ellipticity is defined as 1 - b/a, where a and b represent the major and minor radii of an ellipse. In the case of a circle, ellipticity is equal to zero because a equals to b. A more elongated shape results in a larger ellipticity.
Authors:
・Masakazu A. R. Kobayashi: Research Center for Space and Cosmic Evolution, Ehime University, Japan・Katsuhiro L. Murata: Department of Physics, Nagoya University, Japan
・Anton M. Koekemoer: Space Telescope Science Institute, USA
・Takashi Murayama: Astronomical Institute, Graduate School of Science, Tohoku University, Japan
・Yoshiaki Taniguchi: Research Center for Space and Cosmic Evolution, Ehime University, Japan
・Masaru Kajisawa: Research Center for Space and Cosmic Evolution and Graduate School of Science and Engineering, Ehime University, Japan
・Yasuhiro Shioya: Research Center for Space and Cosmic Evolution, Ehime University, Japan
・Nick Z. Scoville: Department of Astronomy, California Institute of Technology, USA
・Tohru Nagao: Research Center for Space and Cosmic Evolution, Ehime University, Japan
・Peter L. Capak: Department of Astronomy and Spitzer Science Center, California Institute of Technology, USA


