Error budget

Astrophysical noise
Includes stellar activity on the central star and astrometric wobble of background reference stars.
Fundamental measurement noise
Measurement noise due to the primary design parameters such as telescope diameter, pixel sampling and wavelength. This would be equal to the total instrument noise in the absence of defects in the detector or optical train. Includes photon noise contribution from background stars and zodi background.
Static astrometric error terms
Contribution of all static defects, such as poorly calibrated detector response or manufacturing errors in the optical surfaces. Even perfectly static defects produce astrometric errors, as the trajectories of the background stars on the focal plane are slightly different between observations (proper motion, parallax).
Dynamic astrometric error terms
Errors due to changes of the telescope and instrument between observations. Includes variations in the shape of optics surfaces, variations in detector geometry (detector pixels move between observations) and variations in detector sensitivity. Dynamic errors are not fully calibrated by the spikes (spikes have a limited SNR, and do not fully sample the field of view). Dynamic errors can also create errors in the measurement of the spikes positions.

Figure 4-1 lists the main error terms in each of the 4 categories, and provides a more detailed description of their effect on the astrometric measurement accuracy.

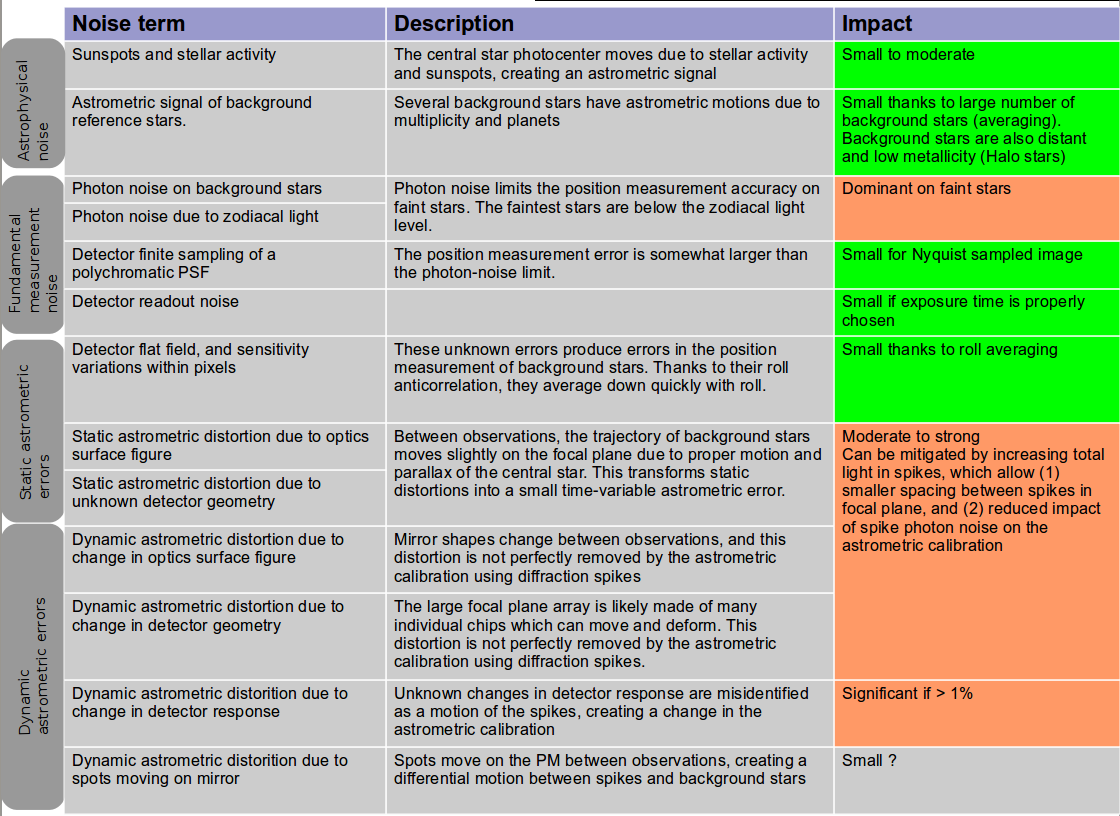Figure 4-1: Overview of main error budget terms. [png]
Error budget terms are divided in 4 categories: astrophysical noise, fundamental measurement noise, static astrometric error terms, and dynamic astrometric error terms.

4.2. Numerical simulations: goals and approach

A numerical simulation was developped to quantify the measurement noise terms outlined in the previous section (all noises except the astrophysical noise). The simulation assumes

1.4m telescope TMA (design by R. Woodruff)
1.5nm surface (3nm WF) optics for M2 and M3, PSD provided by Tinsley for optics of similar size previously manufactured
Circular field of view, 0.2 deg diam (0.03 sq deg)
Stellar density assumed for galactic pole observation (worst case scenario)
Central star is mV=3.7 (faintest of the 7 PECO targets for which an Earth can be imaged in <6hr, 14th brightest target in the 20 high priority targets list)
90% detector peak QE, 80% optical throughput (0.963 for optics reflectivity x 0.92 due to dots on PM)
Nyquist sampled detector at 0.6 micron = 44 mas pixels
Telescope roll = 1 rad (larger angle = better averaging, but more difficult to maintain stability) Single epoch observation = 2 day

The astrometric distortions in the system are computed with 3D raytracing (code written in C, agreement with Code V results from Woodruff has been checked). Focal plane images are produced by Fourier transform, and then distorted according to geometrical optics. Image sizes are 16k x 16k pixel. The telescope and instrument parameters used for the simulation are shown in Figure 4-2, where values are given for the main instrumental sources of measurement errors.

Figure 4-2 shows that the system simulated differs from the final system (which meets the science requirement). The difference is entirely due to computing limitations:the full scale system image sizes would be 40kx40k pixel (>6 GB per image), too large for the fast and easy computation of the astrometric measurement accuracy necessary for parameter optimization and searches (note that all simulations shown here were performed on a laptop computer, and a more powerful computer could perform the computations on a full scale system).

Figure 4-2: Numerical simulation: parameters. [png]
Main telescope and instrument parameter values adopted for the numerical simultion.

The observation of a planet in a 1.2 AU orbit around a Sun-like star at 6 pc is simulated. The source parameters and obervation schedule are detailed in Figure 3-3.

4.3 Numerical simulation details and results

The details of the numerical simulation are given in this set of slides, where each step is described:
Numerical simulation details (pdf)

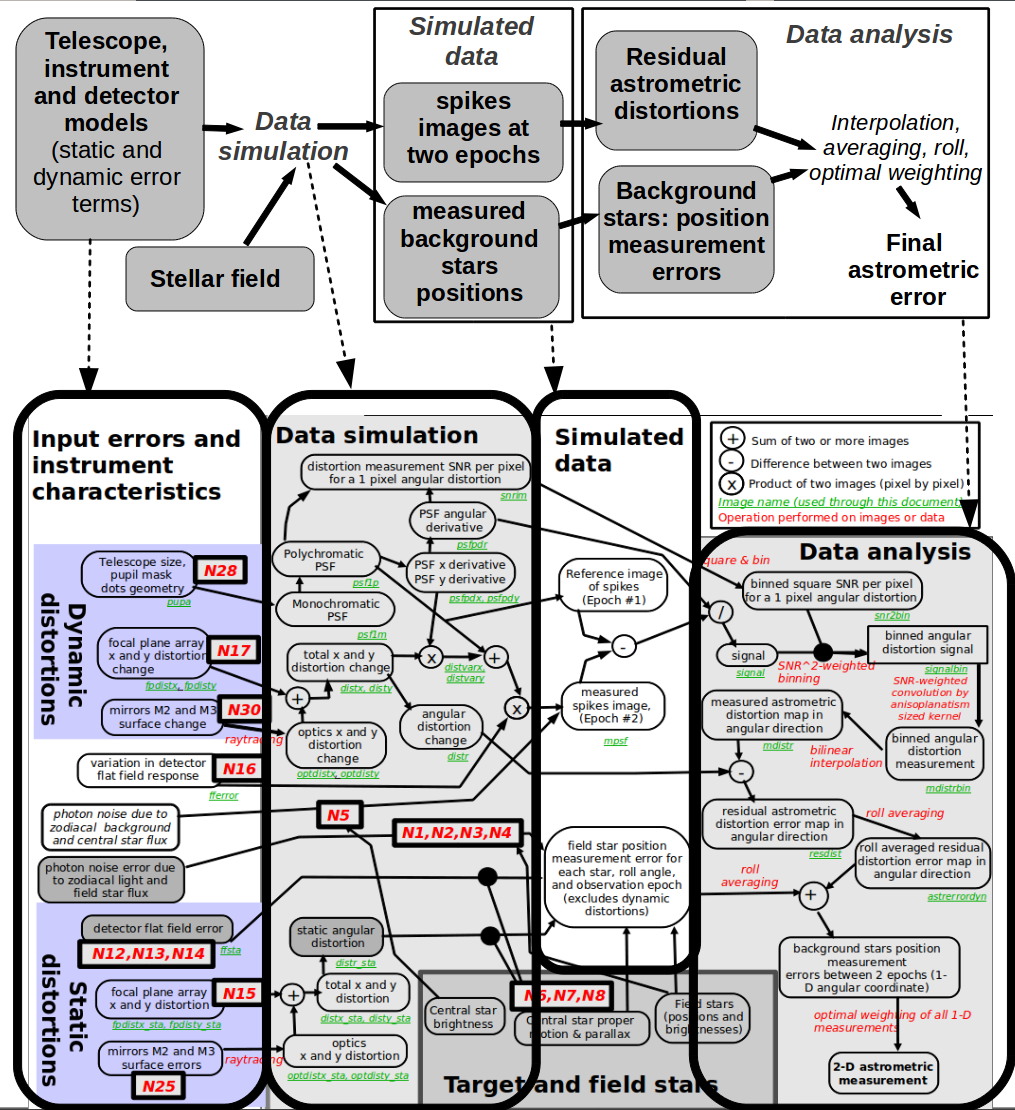Figure 4-2: Numerical simulation overview.
[png]
Detailed block diagram: [png]
List of noise sources (N1 to N30, shown in red on figure): [png]

Key steps in the numerical simulation are described in the pdf document.

The numerical simulation yields a 0.58 μm single-axis astrometric accuracy per measurement.

4.4 Expected astrometric measurement accuracy

According to the numerical simulation, the expected single measurement single axis astrometric measurement accuracy is 0.2 μas for the nominal 0.25 sq deg FOV / 1.4-m diameter telescope system (0.58 μas for the 0.03 sq deg simulated system). Figure 4-3 shows, for the 0.03 sq deg FOV system, that the astrometric measurement accuracy is independant of star brightness for stars brighter than m_V=7, and that it grows for fainter stars. Using simple scaling laws, Figure 4-4 estimates the single measurement astrometric accuracy for a range of telescope diameter and field of view values.

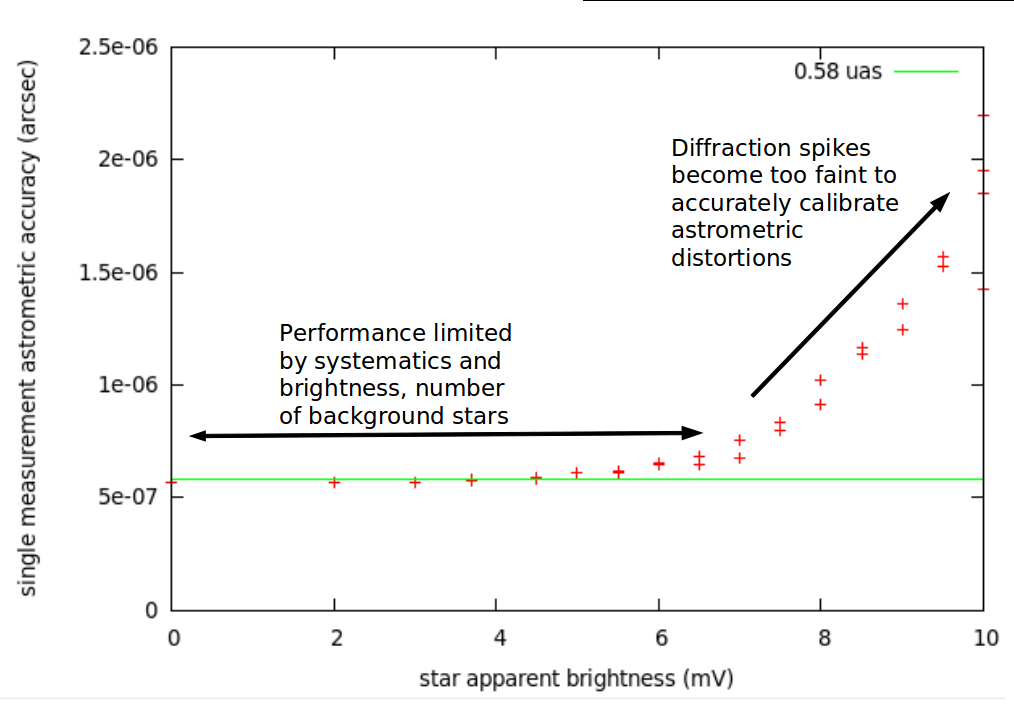Figure 4-3: Single measurement, single axis astrometric measurement accuracy as a function of field of star brightness for the 0.03 sq deg FOV system simulated. [png]

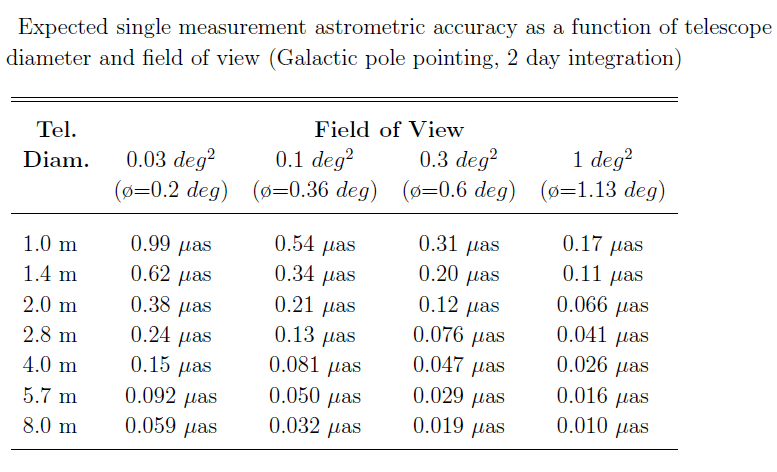Figure 4-4: Single measurement, single axis astrometric measurement accuracy as a function of field of view and telescope diameter. [png]

Astrophysical noise

The astrometric signature of starspots is estimated to be at the tenth of a μas level (Marakov et al. 2009) per measurement.

References

[Makarov et al. 2009] "Starspot Jitter in Photometry, Astrometry, and Radial Velocity Measurements" Makarov, V. V.; Beichman, C. A.; Catanzarite, J. H.; Fischer, D. A.; Lebreton, J.; Malbet, F.; Shao, M., The Astrophysical Journal Letters, Volume 707, Issue 1, pp. L73-L76 (2009) [astro-ph]

Page content last updated: 27/06/2023 06:35:52 HST
html file generated 27/06/2023 06:34:39 HST