Supernullers

---- UNDER CONSTRUCTION ----

Summary

1. Introduction

Direct imaging of exoplanets is scientifically extremely valuable, as physical separation of planet light from the much brighter central starlight is required to acquired high quality spectra of the planet. The combination of high star-to-planet contrast and the small angular separation between the two objects makes this challenging and requires unconventional optical imaging systems, such as coronagraphs or nulling interferometers.

Interferometers are an attractive approach to this challenge, as they are well-suited for high angular resolution, and their beam combiner can be designed to efficiently cancel the central starlight. The non-zero stellar angular diameter must be taken into account for the design of a nulling interferometer, and requires one or more outputs of the interferometer to have maintain a small transmission over the size of the stellar disk. The interferometer's ability to cancel starlight is best quantified by the null depth order γ which describes how transmission evolves as a function of angular distance θ to the optical axis for small angles by approximating it a θ^γ. In most cases, a null order γ=2 is insufficient. For example, in order to keep the starlight level below the planet light level for the observation of a Sun-Earth system analog in the visible (contrast = 1e10, stellar diameter = 1% of planet-to-star separation) requires γ=6 if the Earth is placed at 1 λ/B, and γ=8 if the Earth is placed at 8 λ/B. Deep nulls also offer resilience against pointing errors and reduce exozodiacal light contribution, as the inner part of the exozodiacal cloud is likely to be the brightest.

While the nulling interferometer concept was first proposed with two telescopes and a θ² null, more powerful designs have since been proposed, offering deeper nulls but requiring more subapertures [refs]. Rouan [ref] proposed a technique to achieve arbitrararly deep nulls, provided that a sufficiently large number of telescopes is available. Despite the large number of nulling interferometer designs previously suggested, no clear understanding of how to optimally design nulling interferometers has emerged. A previous study [ref] in fact shows that there exists a minimum null depth order which is only a function of the number of aperture, which we denote γ_min(N), and that for any 2-D interferometer geometry with N apertures, a beam combiner can be designed to produce at least one output with a θ^γ_min(N) transmission near the optical axis.

2. Impact of interferometer geometry on achievable null depth

2.1. Minimum achievable null depth vs. Maximum achievable null depth

As described in detail in the optimal beam combiner study, the optimal null depth in a nulling interferometer can be derived from the Taylor expansion of the complex amplitude at the entrance of the interferometer around the optical axis. For an aperture of the interferometer at position (x,y), the complex amplitude response to a point source at angular position (α,β) is:

ei(αx+βy) = 1 + iαx + iβy - (1/2)(α2x2 + 2αβxy + β2y2) - (i/6)(α3x3 - 3α2βx2y - 3αβ2xy2 - β3y3) + ....	(2.1)

To each point on the sky corresponds a N-coefficient vector V(α,β) of complex amplitudes representing the input of the interferometer across the N apertures. The coefficients of this vector are:

V_k(α,β) = rk (1 + xk (i α) + yk (i β) - xk2 (α2/2) + xkyk (αβ) + yk2 (β2/2) - (i/6)(α3xk3 - 3α2βxk2y - 3αβ2xkyk2 - β3yk3) + ... )	(2.2)

Where r_k is the radius of aperture k (or the square root of its collecting area, if not circular). A stellar disk of finite diameter is approximated as a series of NBpt mutually incoherent point sources covering the stellar disk, and the corresponding interferometer input is then represented by NBpt vectors. The optimal nulling beam combiner design is obtained by matching the terms of this expansion with the interferometer outputs. Thus, in the general 2-D case, the brightest output of the nulling interferometer should coherently mix inputs with coefficients r_k, concentrating most of the starlight. The next two outputs will remove from the expansion the first order terms in x and y, thus producing second order nulls in intensity (square of first order nulls in amplitude). Provided that the number of apertures is sufficiently large to access these modes, the next 3 modes will remove the terms in x², y² and xy, and will therefore be fourth-order nulls in intensity. This process is continued until the number of modes reaches the number of apertures in the array, and therefore produces a well-defined relationship between the number of apertures N and the achiveable null depth γ_min(N).

2.2. Maximum null depth, and condition for achieving a supernull

A matrix notation of the N-aperture interferometer geometry is defined in this section, with

             | 1 x0 y0 x0^2 x0x0 y0^2 ...|
             | 1 x1 y1 x1^2 x1x1 y1^2 ...|
Mgeom(N,L) = | ..........................|
             | 1 xk yk xk^2 xkxk yk^2 ...|
             | ..........................|

To achieve a supernull, the interferometer geometry must be such that terms in the Tailor expansion given in equation (2.2) are linearly dependent. Mathematically, this is equivalent to the rank of the matrix M_geom(N,N) being strictly less than N. This allows a mode of the interferometer beam combiner to simultaneously suppress more than a single term of the Taylor expansion, therefore potentially reaching deeper null depth than possible if no linear combination exists between the columns of M_geom(N,N). Additional orders of the Taylor expansion can then be reached, as can be represented by M_geom(N,L) with L>N.

The maximum null depth of the interferometer is:

γmax(N) = γmin(L)	(2.3)

with L chosen such that the rank of M_geom(N,L) is equal to N:

rk(Mgeom(N,L)) = N	(2.4)

Equation (2.3) and (2.4) show that the maximum achievable null depth for a given interferometer geometry is determined by counting the number of terms in the Taylor expansion given equation (2.2) that can be cancelled by the first N-1 outputs of the interferometer, and measuring the order of the remaining Nth term. If linear dependencies exist in the first columns of matrix M_geom(N,N), then additional column(s) can be added to the matrix until the rank of M_geom(N,L) is equal to N, corresponding to a beam combiner with N outputs able to match the first L terms of the Taylor expansion. The maximum null depth is then given by the order of the last column of M_geom(N,L).

3. Types of supernuller geometries

3.1. Linear arrays

3.2. Circular arrays

In a circular array, the apertures coordinate (x,y) follow a relationship of the type x²+y²=r². This relationship introduces linear dependencies in the columns of matrix M_geom through the following relationships:

y2 = x2 - r x y2 = x3 - rx y3 = x2y - ry x2 y2 = x4 - rx2 xy3 = x3y - rx ...	(3.1)

As can be seen from these relationships, any x^k1y^k2 with k2>1 can be written as a linear combination of x^k1'y^k2' terms with k2'=0 or 1. For each fixed value of (k1+k2), there is therefore only two linearly independent columns in the matrix. To obtain rk(M_geom(N,L))=N, the highest order terms in the matrix must be k1+k2=floor(N/2). This analysis therefore predicts that the achievable null order for any circular array is:

γcirc(N) = 2 floor(N/2)	(3.2)

For example, any circular array with N=8 should offer a θ⁸ null, while a random 2-D geometry with the same number of apertures is limited to a θ⁶ null.

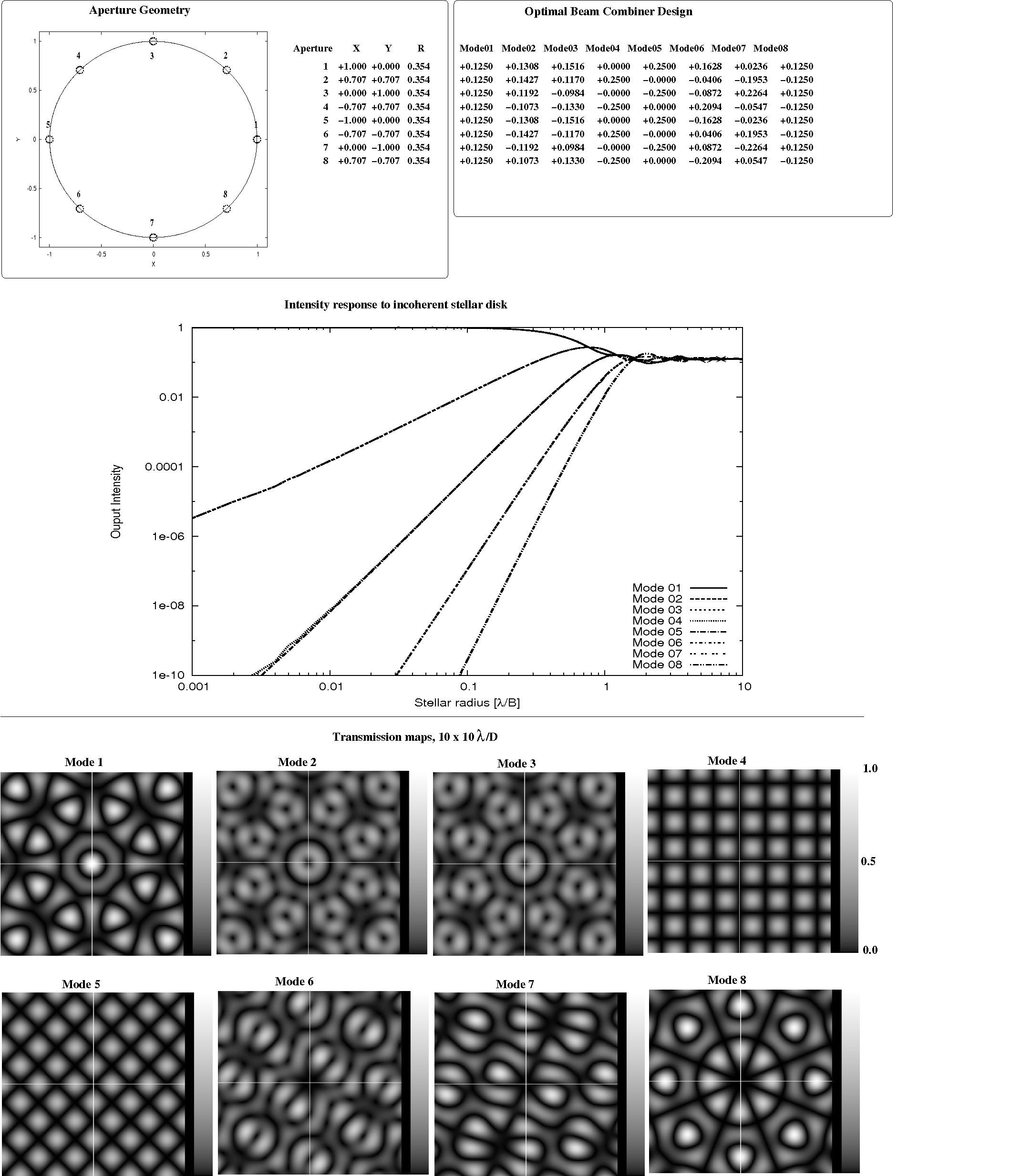
Fig 3.1: Optimal beam combiner solution for a 8-aperture regular octogon array geometry, computed here for a 0.001 λ/B stellar radius. [eps]

3.3. Other geometries

Other relationships between the x and y coordinates of the subapertures can produce linear dependencies between the columns of M_geom. Several of them are listed in table 1, and the analysis presented in sections 3.1 and 3.2 can be generalized to these other geometries. Figure 3.2 shows, for the geometries lists in table 1, how null depth order improves as the number of apertures N increases. Linear arrays offer the best null depth for a fixed number of aperture. Cicular geometries (circle, ellipse, arc) and hyperbola geometry offer better null depth than random 2-D geometries for N=6 and N>7. Any point on this figure above the thick curve indicating the general 2-D case is by definition a supernuller.

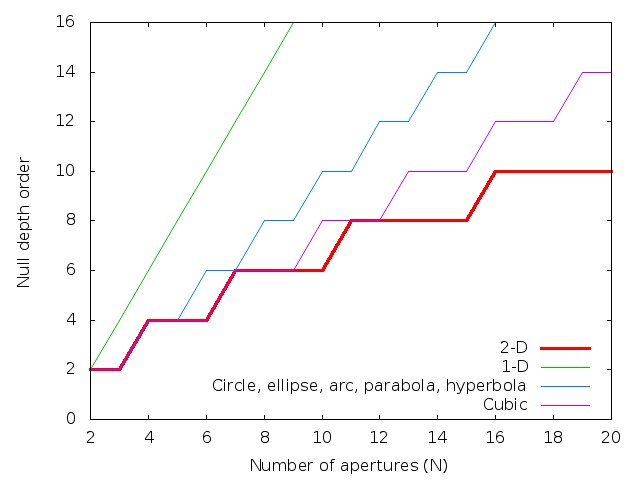Fig 3.2: Null depth order as a function of number of subapertures for different array geometries. [eps]

For example, if apertures are on an hyperbola following the relationship xy=a, then any x^k1y^k2 with k1>1 and k2>1 can be written as a linear combination of terms in the form x^k1'y^k2' with k1'=0 or k2'=0. Just as for the circle array geometry, for each fixed value of (k1+k2), there is therefore only two linearly independent columns in the matrix. The null depth achievable with any hyperbola array geometry is therefore:

γhyperb(N) = 2 floor(N/2)	(3.3)

Figure 3.3. illustrates this finding by showing a 6-aperture hyperbola array geometry achieving a θ⁸ null. This null depth is not achievable in the general 2-D case, so the interferometer qualifies as a supernuller.

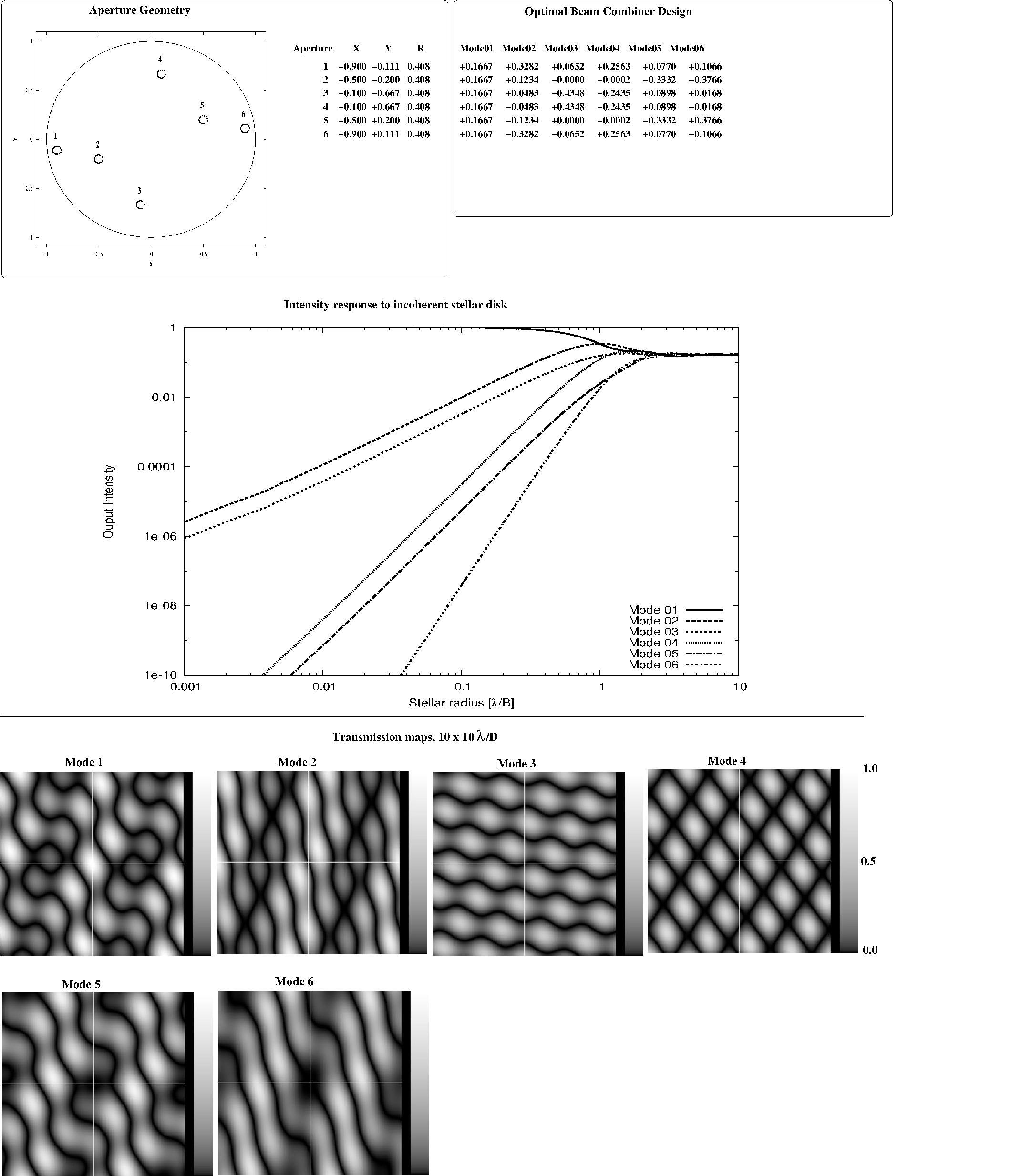Fig 3.3: Optimal beam combiner solution for a 6-aperture hyperbola array geometry, computed here for a 0.001 λ/B stellar radius. [eps]

Conclusions

A previous study showed the existence of a minimum achievable null depth, and showed that linear arrays arrays can achieve considerably deeper nulls than non-linear arrays with the same number of apertures. The study presented in this paper completes this work by quantifying the maximum null depth achievable as a function of array geometry. A key finding is that several simple 2-D geometries (circle, parabola, hyperbola) offer deeper nulls than possible with a general 2-D geometry. These supernullers can offer particularly effective solutions for high contrast imaging of faint exoplanets around partially resovled bright stars. Incidentally, the circle (or arc) geometry, in addition to being a family of supernullers, allows easy beam combination without requiring large delay lines if light is mixed in a central hub.

The design of a nulling interferometer must take into account many parameters in addition to null depth, such as sensitivity to background light, (u,v) plane coverage, tolerance to noise sources, and array efficiency. The work presented in this study is therefore not intended to directly lead to sensible nulling interferometer designs, but it is expected that nulling interferometer geometries should tend to be supernullers if null depth is a performance driver, and if no other strong constraint forces the subapertures positions.