Appendix A. Fundamental Limitations of diffraction-limited imaging astrometry

In this section, the fundamental (no distortions, perfect noiseless detector) limits of astrometric accuracy are reviewed.

A.1. Astrometric accuracy at the diffraction limit

With an ideal telescope (no wavefront aberration, no central obstruction), the accuracy with which a monochromatic PSF (exact Airy function) can be localized in 2D is, in the photon-noise regime:
σ2D [λ/D] = sqrt(2)/(π sqrt(Nph)) = 0.450/sqrt(Nph) (equ A.1.1)
where D is the telescope diameter, λ is the wavelength and Nph is the total number of photon available for the measurement.
If the PSF position is measured along one axis only, the measurement error is:
σ1D [λ/D] = 1/(π sqrt(Nph)) = 0.318/sqrt(Nph) (equ A.1.2)

These measurement accuracies are obtained with an optimal matched filter which optimally weights each pixel according to SNR. Numerically these equations can be verified by starting from the PSF (noted PSF(x,y)) and computing:
(1/σx)2 = SUMx,y (1/σpixel x,y)2 = SUMx,y( (d(PSF(x,y))/dx)2 / PSF(x,y) ) (equ A.1.3)

with σ1D=σx=σy, and σ2D = sqrt(2)*σ1D. Equation (A.1.3) shows for each pixel the signal (equal to d(PSF(x,y))/dx) and the noise (equal to sqrt(PSF(x,y)).

A.2. Chromaticity and photon noise

Equations (A.1.1) and (A.1.2) above assume a monochromatic PSF, but a real polychromatic PSF is not as sharp (see fig A-1) and will lead to a lower astrometric accuracy for the same total number of photon (see fig A-2). This performance loss is however modest, especially compared to the sensitivity gain offered by including more flux as the spectral bandwidth increases. Figure A-2 shows that with a 50% spectral bandwidth (x~0.25), the astrometric error is 38% more than it would be in monochromatic light with the same number of photon.
Fig A-1: Impact of spectral bandwidth on PSF shape. [jpg]
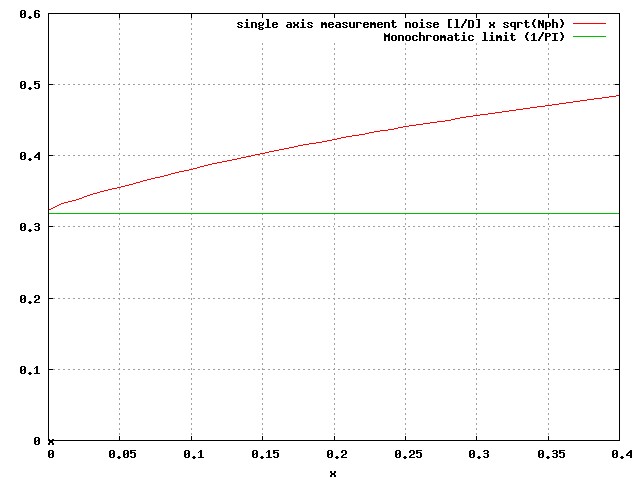
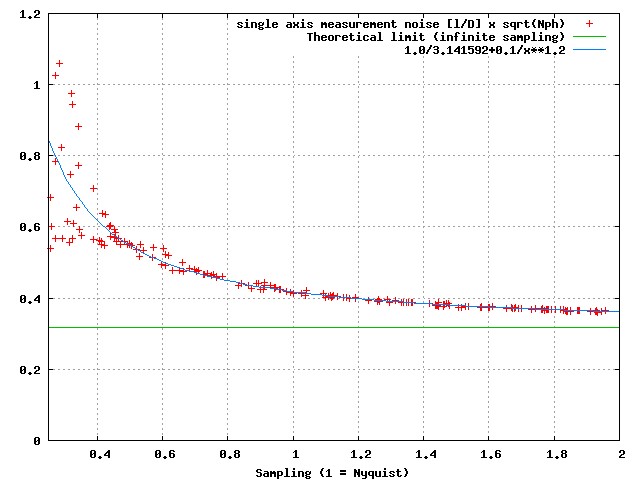
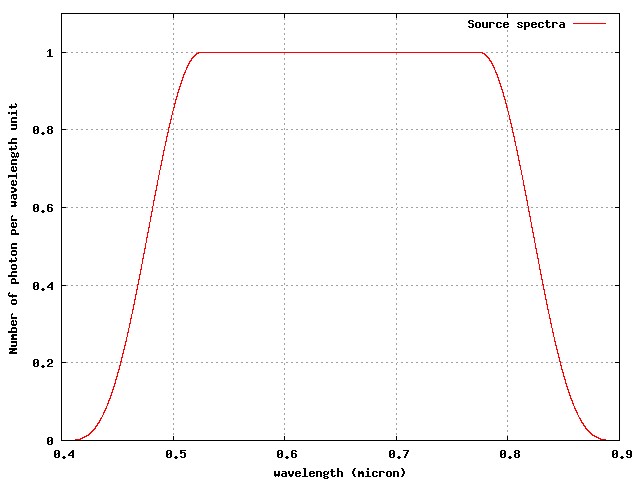
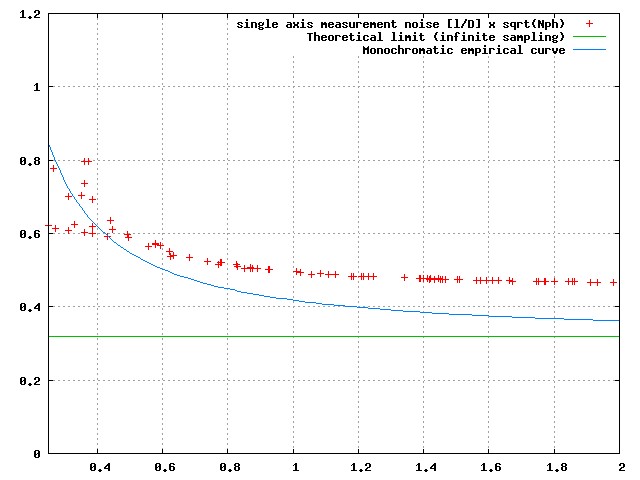
Monochromatic PSF (top left), x = 0.1 (top right, approximately 20% wide spectral band), x = 0.2 (bottom left, approximately 40% wide spectral band) and x = 0.4 (bottom left, approximately 80% spectral band). In each case, the spectra is flat in dlambda, and extends from lambda0/(1+x) to lambda0*(1+x). The sampling is 10x Nyquist at the central wavelength.
Fig A-2: Loss of photon noise limited astrometric measurement accuracy as x (roughly equal to half the spectral bandwidth) increases. [jpg] [ASCII data]
The data was computed at 10x Nyquist at the central wavelength, with equation (A.1.3) used to compute the astrometric error due to photon noise. Polychromatic PSFs are computed as an incoherent sum of 50 monochromatic PSFs, each scaled to the same physical plate scale.

A.3. Detector sampling

In sections A.1. and A.2., a perfect detector with infinite sampling was considered.
Fig A-3: Example PSFs with different detector sampling. [jpg]
0.5x Nyquist (top left), 1x Nyquist (top right), 2x Nyquist (bottom left) and 4x Nyquist (bottom left). In each case, the PSF is monochromatic and the PSF center is randomly set to a non-integer pixel coordinate.
Fig A-4: Single axis photon noise limited astrometric measurement accuracy as a function of detector sampling. [jpg] [ASCII data]
Monochromatic simulation. At small sampling, the points fan out between a lower boundary corresponding to the "quad cell" case where the PSF center falls at the corner of 4 pixels (and the astrometric error becomes independent of sampling, as shown by the flatness of this lower boundary), and an upper boundary where the PSF is centered on a pixel.
The astrometric error induced by photon noise is well described by the following equation, derived empirically from the points in Figure A-4, and is shown in blue on the figure:
σ1D [λ/D] = (1/sqrt(Nph)) x (1/π + 0.1 x SamplingFactor-1.2) (equ A.3.1)
where SamplingFactor is 0.5 times the linear number of pixel per λ/D, and is therefore equal to 1 for Nyquist sampling (SamplingFactor = 1.5 means 3 pixel per λ/D). Figure A-4 clearly shows that astrometric accuracy in the photon noise regime continues to improve as the sampling increases beyond the Nyquist limit. Provided that a good model of the PSF exists, the astrometric accuracy remains quite good below Nyquist sampling: at 0.4x Nyquist (pixel linear size > λ/D), the 2-D astrometric accuracy is still below 1/sqrt(Nph) λ/D. Below 0.4 Nyquist, the astrometric accuracy is a function of the exact PSF location, with optimal sensitivity when the PSF falls on the corner between pixels.
Fig A-5: Spectra adopted for this work (number of photon per wavelength unit). [jpg]
The spectra covers the 0.4 to 0.6 micron region. Half of the number of photon is at λ<0.65μm. Half of the energy is contained at λ<0.625μm. When listing angles in λ/D unit in this document, λ is assumed to be 0.6 μm.
Fig A-6: Single axis photon noise limited astrometric measurement accuracy as a function of detector sampling for a polychromatic measurement (with the spectra shown in Figure A-5). [jpg] [ASCII data]
There is little gain beyond Nyquist sampling.

A.4. Wavefront errors and optimal PSF shape for astrometry

A.4.1. Astrometric sensitivity in the presence of low order Zernike wavefront errors

Figure A-7 shows that, in monochromatic light, some wavefront aberrations can be introduced with no loss in astrometric sensitivity, while other wavefront aberrations considerably reduce astrometric sensitivity (for example Focus). This behavior is also observed to some extent in polychromatic light (Figure A-8). The wide field corrector for the camera can therefore be designed more easily, as moderate amount of residual coma will not seriously affect performance.
Fig A-7: 1D Photon noise limited astrometric accuracy in the presence of wavefront aberrations (monochromatic light). [jpg]
Simulation performed with sampling = 2x Nyquist.
Fig A-8: 1D Photon noise limited astrometric accuracy in the presence of wavefront aberrations (polychromatic light). [jpg]
Simulation performed with sampling = 2x Nyquist.
Fig A-9: Monochromatic PSF with 2 rad RMS trefoil aberration. [jpg]
As shown in Figure A-7, this aberration does not reduce astrometric accuracy in monochromatic light: in the photon noise limit, the astrometric measurement will be as accurate as for a perfect PSF (Airy pattern). In polychromatic light, Figure A-8 shows that astrometric sensitivity is slightly reduced with this aberration.

A.4.2. Optimal PSF choice

A PSF where the flux is distributed across many pixels can reduce the astrometric measurement errors due to detector defects, and allows brighter stars to be observed without reaching detector saturation. Results obtained in section A.4.1 suggest that it may be possible to obtain such a PSF with little loss in sensitivity to photon noise.