Non-linear Curvature Wavefront sensing
1. Principle
The non-linear Curvature wavefront sensor (nlCWFS) uses 4 defocused pupil images to measure with great sensitivity wavefront aberrations. It is derived from phase diversity wavefront sensing. Thanks to the presence of diffraction-limited speckles in the defocused pupil images, the sensor measures wavefront errors with the sensitivity given by the diffraction limit of the telescope, instead of the sensitivity given by the seeing limit for most common wavefront sensors.
A detailed description of the wavefront sensor and its performance can be found in this paper: "High Sensitivity Wavefront Sensing with a non-linear Curvature Wavefront Sensor" [pdf][astro-ph], Guyon, O. PASP, 122, pp.49-62 (2010).
 |
Simulated closed loop images with Shack-Hartmann and non-linear curvature wavefront sensors. No phase plate was included in the nlCWFS for this simulation.
[jpg]
[eps]
|
2. Optical configuration
2.1. Example of a possible optical layout
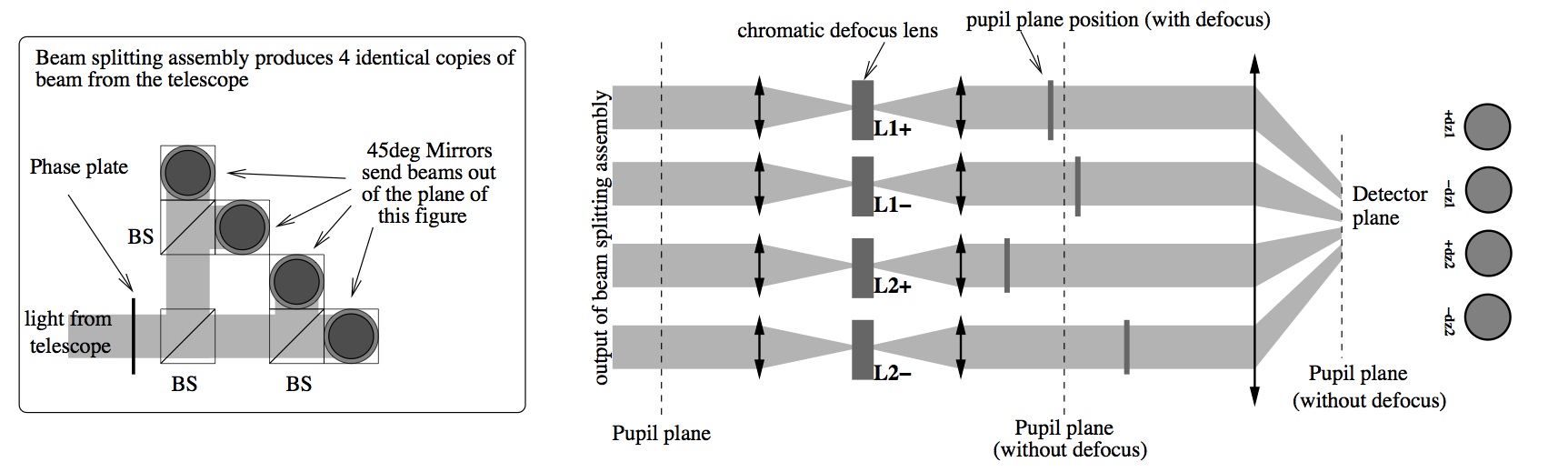
The nlCWFS needs to produce 4 defocused images of the pupil. each conjugated to a different plane (2 images are conjugated ahead of the pupil, 2 images are conjugated after the pupil).
2.2. Chromaticity
For each of the 4 images, the distance between the plane to which the image is conjugated to be pupil plane needs to be inversely proportional to the wavelength. This is necessary to maintain sharp diffraction-limited speckles in broadband light.
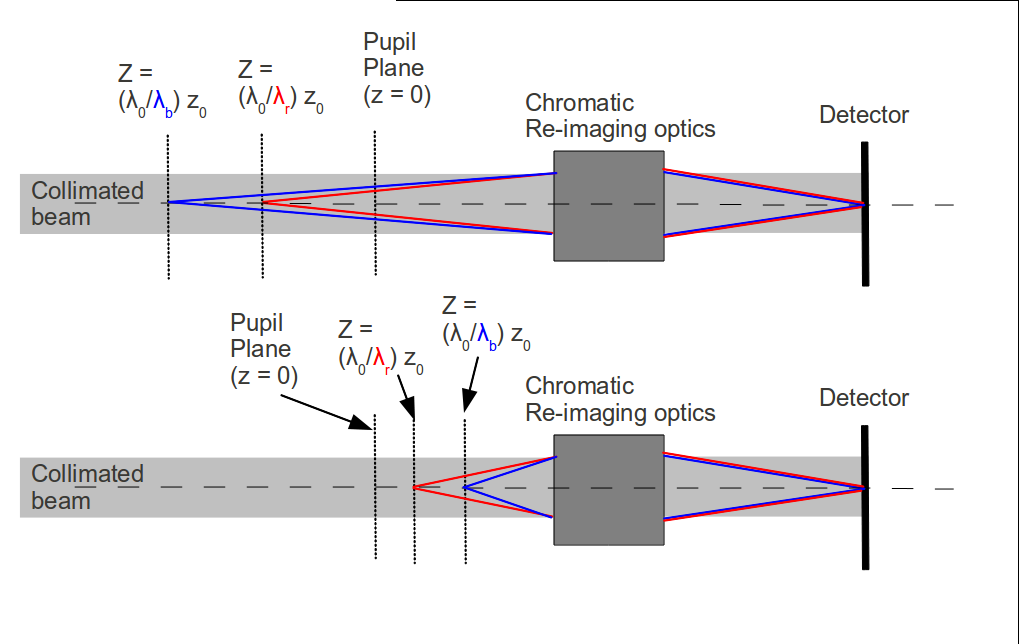 |
Chromatic compensation within the nlCWFS: principle of chromatic compensation
[png]
[ppt]
|
 |
Chromatic compensation within the nlCWFS
[jpg]
[eps]
|
3. Reconstruction algorithm
3.1. Iterative GS-type reconstruction
The nlCWFS wavefront reconstruction requires a non-linear wavefront reconstruction algorithm. The iterative reconstruction algorithm used so far for nlCWFS research can be found on this webpage.
3.2. Required computing power
The reconstruction algorithm is performing iterative GS loops. In closed loop, approximately 10 loops are required per AO loop iteration. Assuming pupil is 32 pixels across, the required number of operations per GS iterations are:
- 8 complex FFTs, each 64x64 pixels, single precision (the geometrical pupil is 32 pixels, and the FFT array size need to be double the pupil size)
- 4 transformations from (real, imaginary) to (amplitude, phase) of 32x32 single precision images
- 4 transformations from (amplitude, phase) to (real, imaginary) of 32x32 single precision images
This work is supported by the National Science Fundation (NSF) and the National Astronomical Observatory of Japan (NAOJ), and NASA.